Go Proxy Security, Part 2: In the Tree

Tuesday, 4. July 2023

In Part 1 of this series, I explained why Go offers a module proxy and that it is secured by the gosumdb. In this part, I explain how gosumdb secures the Go proxy.

If you want to trust the authorship of code, you would need a direct trust relationship with the code author. In a highly dynamic module ecosystem like Go, this would be infeasible. The assumption that gosumdb makes is, if everyone looks at the same code, it must be the right code.

The module path together with the version is unique (for example github.com/restic/restic@v0.15.2). When pulling it via the Go module proxy, it is trust on first use. It doesn’t matter who uses it first. Trust on anyone’s first use.

Checksum of a module

A Go module has two checksums: One for all files in the repository and another checksum just for the go.mod file. The go.mod file is treated separately because it speeds up dependency resolution when it is read independently from the rest of the code.

Gosumdb works as a global repository for all go.sum entries. You can look at the first 256 entries with an HTTP GET request with curl https://sum.golang.org/tile/8/data/000

golang.org/x/text v0.3.0 h1:g61tztE5qeGQ89tm6NTjjM9VPIm088od1l6aSorWRWg=
golang.org/x/text v0.3.0/go.mod h1:NqM8EUOU14njkJ3fqMW+pc6Ldnwhi/IjpwHt7yyuwOQ=

golang.org/x/crypto v0.0.0-20190404164418-38d8ce5564a5 h1:bselrhR0Or1vomJZC8ZIjWtbDmn9OYFLX5Ik9alpJpE=
golang.org/x/crypto v0.0.0-20190404164418-38d8ce5564a5/go.mod h1:WFFai1msRO1wXaEeE5yQxYXgSfI8pQAWXbQop6sCtWE=
...

Here we have per line

A unique identifier (path and version)
Hash method h1, which refers to sha256
Hash

The code for calculating module hashes is here

Two lines always belong together. These two lines are hashed and this hash is the respective entry in the gosumdb.

Remember (from part 1) that the underlying Merkle Tree is an append-only log, so the order of entries matters. That makes numbering entries easy. Every block of two lines is identified by a strictly increasing number.

As an example, we can look up an entry in the gosumdb.

curl 'sum.golang.org/lookup/github.com/restic/restic@v0.15.2'
17204294
github.com/restic/restic v0.15.2 h1:VTHI10VxE7hiJuYk1ptr67RyuuWKbUNuUOsSh2/RU+s=
github.com/restic/restic v0.15.2/go.mod h1:6MxBaAanCURFzuf7vfE7rXMSSPyi3ABJysJfPaA5kKE=

go.sum database tree
18239807
e91VsqvXSwaz3PwX4jwUBt2wMYZ++OMwbKi+h7Hg63Y=

— sum.golang.org Az3grooXqMrJDeBKRd4k8nuh8SsvP6BSKIWGqlOH13f8DMULyJD7vqUmYDqvOywI2ssdyrTLzE2wqX6/olE8q+xh8wY=

Restic at version 0.15.2 is the 17.204.294th entry.

Below the two entries for restic, you see another 4 lines of text, including the number of entries in the tree at a moment in time after this version of restic was added to the tree. The line of gibberish is the root hash. In the next section, I’ll describe how the root hash is calculated.

The last line is the cryptographic signature from sum.golang.org for the given hash.

The question is: Does everyone else see this? Could someone secretly exchange the contents of restic at this version, and serve a different lookup to us, so we see something else?

I expected to find the public key for sum.golang.org more easily. I eventually found it in the go source code. I wished there was a more prominent placement. Let me know if you know another source for the public key.

Merkle Trees and the Tree Head Hash

There is a good explanation of Merkle Trees and the calculation of Tree Head Hashes written by Google.

I will not re-write what they have already written. What is important to understand is that the Tree Head Hash is always implicitly contained in the Merkle Tree because it can always be calculated with access to the leaf hashes.

That means with access to all leaves, I can calculate a Tree Head Hash for a given moment, based on the number of entries in the Tree. As of writing this paragraph, the gosumdb has 18.240.282 entries. Clients that want to download and verify these entries would need a lot of bandwidth and computing power.

To avoid the burden on servers and clients, gosumdb uses a trick to reduce storage and processing times. Each part of the db is chunked into 256 entries. These chunks are called tiles.

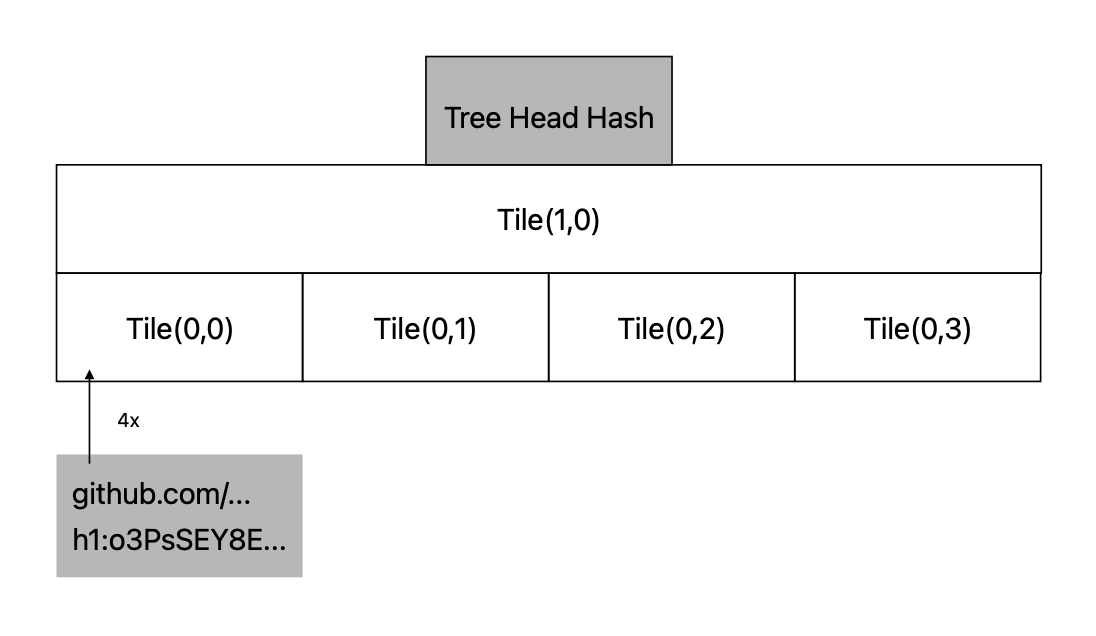
Merkle Tree Tiles

The image is a schematic example for tiling. Instead of 8 levels as used in the go mod implementation, it shows 2 levels per tile with 4 inputs each.

Tiles have 8 virtual levels (lengths: 256, 128, 64, 32, 16, 8, 4, 2). Each level builds the foundation for the next higher level. Because 2 entries build one entry in the next higher level, the number of entries is half for the next higher level. The highest two entries, hashed together, can be found in the next tile. The next higher tile consists of 256 entries again, as well with 8 levels.

What about unbalanced tiles? Not every Tree Head Hash needs to originate from a perfectly balanced tree. If a tree does not have a “power-of-2” number of entries, the algorithm is as follows:

For the given number of entries, create the sum of decreasing powers-of-2 for this number. Example 7 entries: 4+2+1 = 7, with each addend being a power-of-2 in strictly decreasing order.

Calculate the Tree Head Hash for every sub-tree, left to right. Example: “a”, “b”, “c”.

Use each Tree Head Hash and calculate the final Tree Head Hash from right to left. Example: hash(“a”, hash(“b”, " c")) = Tree Head Hash.

With this logic, it takes only a few tiles to compute the Tree Head Hash. The size of 8 levels is a sweet spot. In the original paper the authors explain that a height starting at 4 levels makes sense. It is a tradeoff between the number of tiles to download, used storage space, and computational complexity.

The hashes for the leaves are computed differently than the hashes for every other level. This is due to the vulnerability of Merkle Trees to the second preimage attack that works as follows:

Given an entry “a” with hash(“a”) = “h1” and entry “b” with hash(“b”) = “h2”. For the next level in the Merkle Tree, we would calculate hash(“h1+h2”) = “h3”. Now imagine an attacker feeding an entry with “h1+h2”, which would give an entry for hash(“h1+h2”) = “h3”. An attacker could freely create valid hashes for the leaves, and even replicate the Tree Head Hash, which is signed.

This attack is prevented by prefixing leaf hashes differently than other levels in the Merkle Tree. For example hash(“leaf+a”) for a leaf entry and hash(“m+h1+h2”) for all composed hashes in the Merkle Tree.

This is explained in https://www.rfc-editor.org/rfc/rfc6962.html#section-2.1

How it all works together

After including a module in Go, the source code is downloaded from the proxy. Go will lookup and retrieve the go.sum entries. The hashes for go.sum are verified against the downloaded source code.

Now we have a connection between the source code and an entry (the two lines of go.sum) from gosumdb.

Next, Go verifies that the entry for go.sum is really in the gosumdb. The entry can be hashed. This hash has to be present in one of the tiles containing all leaves, so Go downloads the respective tile and verifies that the hash is in it.

Now we only have to prove that the signed Tree Head Hash matches the calculation we do ourselves for the Tree Head Hash. For that, Go needs to download a few missing tiles to complete the tree and calculate the Tree Head Hash.

Because the Merkle Tree is verifiable append-only, and we have parts of the tree cached locally, we can be sure the logic of hashing adds up. Unless there is a targeted attack that serves us a different Merkle Tree than anyone else, from the start and forever, we know we see the code everyone else sees.

How can we trust other tiles?

You might wonder how an entry in the leaf and the Tree Head Hash come together when all other tiles look a bit arbitrary in the data they contain.

The used hashing function sha256 is resistant to preimage attacks. That means, given a Tree Head Hash, it is infeasible to create tiles that would create the Tree Head Hash. We have to put all our trust into the preimage resistance to implicitly trust the served tiles. Sha256 could one day be vulnerable to preimage attacks if someone discovers a way to choose a message for a given hash. That’s why gosumdb prefixes hashes with “h1:” so that a better hash function can be used in the future, probably prefixed with “h2:”.

Outlook for Part 3 of this series

Not every Go developer needs to know the details of the integrity of the Go proxy. Still, the majority of Go developers rely on this integrity. In the third and last part of this series, I’ll introduce an auditing tool that I wrote, which verifies the integrity of gosumdb and goes beyond the checks that Go itself performs.